상관관계 분석(Correlation analysis)의 여러 분파들
지난 시간에는 상관관계 분석에서 가장 보편적으로 사용되는 피어슨의 r에 대해 알아봤습니다.
2022.08.11 - [데이터과학 기초/통계] - 파이썬으로 상관관계(Correlation analysis) 분석하기 : 피어슨의 r
이 포스팅에서는 피어슨의 r을 소개하면서 반복적으로 "연속형 변수"라는 말을 강조했습니다.
이는 "연속형 변수(Continuous Variable)"와 "서열형 변수(Ordinal Variable)"의 속성 차이가 결과에 크게 영향을 미치는 데도 불구하고 현실에서 잘못 사용되거나, 혼용되는 경우가 많기 때문입니다.
오늘은 "서열형 변수(Ordinal Variable)"의 상관관계 분석을 위한 "스피어만의 ρ (Spearman's rho)"와 "켄달의 τ (Kendall's τ)"에 대해 알아보면서 이 차이를 구체적으로 설명하겠습니다.
서열형 변수(Ordinal Variable)?
서열형 변수는 말 그대로 "순서"를 기록한 숫자라고 볼 수 있습니다.
연속형 변수와 유사한 형태를 갖고 있지만, "분절"된 형태를 갖고 있는 점이 특징입니다.
예를 들어 설문을 진행할 때, 나이를 그대로 기입한다면(19살, 28살, 33살 등...) 연속형 변수입니다.
하지만, 나중에 연령별 구간(10~19세, 20~29세, 30~39세...)으로 나눈다면 서열형 변수가 됩니다.
이렇게 나눌 경우 연속형 변수와 비교하여 자료의 해상도가 떨어질 수 있지만, 큰 범위의 값을 축소된 범위 단위로 요약해서 확인할 수 있는 장점을 갖게 됩니다.
(다만, 이렇게 변환할 경우 (연속 -> 서열)의 변환은 가능하지만 (서열 -> 연속)의 변환은 불가능하다는 문제가 있습니다)
둘 사이의 구분이 헷갈리는 이유는 대부분의 서베이 결과 분석에서 연속형 변수와 서열형 변수를 혼합해서 사용하기 때문입니다.
특히, 분할된 데이터를 "순위(rank)"로 볼것인가 "순서(order)"로 볼 것인지에 따라 방법론을 나눠 적용하는 경우도 많습니다.
(오늘은 자료 형태에 대한 고찰이 아니기 때문에, 이 부분은 넘어가도록 하겠습니다)
데이터
오늘의 가상 데이터는 "소득 수준"과 "취미 시간" 의 두 데이터를 사용한 분석을 해 보겠습니다.
소득 수준은 (1단계~5단계까지), 취미 시간 또한 (1단계~5단계까지)로 설정하겠습니다.
또한, 1의 경우 가장 낮은 수준, 5의 경우 가장 높은 수준으로 설정하겠습니다.
데이터는 아래와 같이 다운받을 수 있습니다.
데이터를 파이썬 폴더에 위치시킨 후, 제대로 로드됐는지 확인하고 분석을 시작하면 되겠습니다.
import pandas as pd
times = pd.read_csv("./times.csv")
times.head()

데이터 탐색 / 시각화
소득수준이나, 취미 시간의 경우 모두 등급으로 나눠져 있어 연속형으로 보기 쉽지만 실제로는 "서로 나눠진 수준"을 갖고 있습니다.
그렇기 때문에, 일반적인 연속형 변수의 속성을 보여주는 describe()의 해석에서 조심할 필요가 있습니다.
times.describe()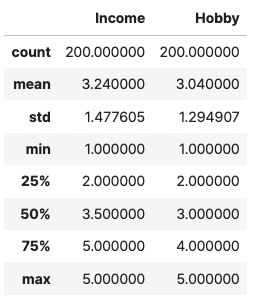
해당 데이터의 값은 등급 구분이기 때문에 3.24나 3.04라는 소득 수준은 존재할 수 없기 때문입니다.
(연령대로 서베이를 할 때 20대, 30대는 존재하지만 25대 라는 구간은 존재할 수 없다고 생각하면 되겠습니다)
그렇기 때문에, 이 경우는 빈도를 보는 value_counts()를 사용해야 정확한 특징을 볼 수 있습니다.
value_counts()는 지정한 컬럼의 요인 개수를 세주는 기능입니다.

이제 Hobby 컬럼에도 적용해 볼까요?

value_counts()를 사용하는 이유는 1,2,3,4,5... 와 같은 데이터가 구분된 속성을 갖고 있기 때문에 연산을 하는 것이 의미가 없기 때문입니다.
이것은 시각화 과정에서도 나타납니다.
피어슨의 r을 구하는 과정에서 사용했던 산포도(scatter plot)를 확인해 봅시다.
import seaborn as sns
sns.scatterplot(data=times, x="Income", y="Hobby")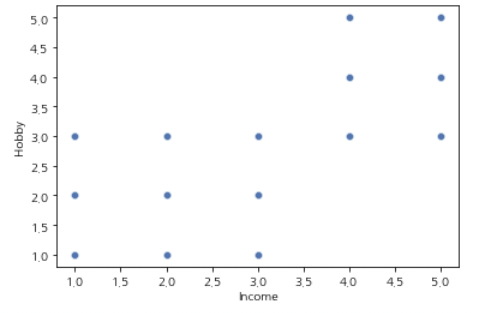
산포도 결과는 일정한 경향성을 보여주지만, 연속형 변수처럼 각각의 특성을 해석하기 어렵습니다.
각 값이 실제 값이 아닌 등급을 포함하고 있기 때문입니다.
그렇기 때문에, 등급별 데이터의 경우 히스토그램 등 유저가 원하는 방향의 추가적 해석을 수행할 필요가 있습니다.
sns.displot(times.Income,kde=True)
sns.displot(times.Hobby,kde=True)

(kde 옵션은 굳이 필요없지만, 이전 포스팅과 연속성을 위해 넣어 놓았습니다)
이제, 데이터가 갖는 특징을 파악했으니 실제 통계적 검정 과정으로 넘어가겠습니다.
비모수 검정(Non-parametric test)의 조건
지금까지 우리가 해온 t-test 등은 모두 모수 검정(Parametric Test)과 깊은 관계를 갖고 있었습니다.
모수 검정은 기본적으로 데이터가 "특정 조건(정규분포 등)"을 만족해야 사용할 수 있는 분석입니다.
(모수에 대한 가정은 나중에 통계의 해석 방식에서 구체적으로 다루도록 하겠습니다)
반대로, "등급 데이터"와 같이 연속되지 않은 데이터의 검정에서 우리는 비모수 검정(Non-Parametric Test)을 사용할 수 있습니다.
이 경우, 요구 조건이 사라지게 됩니다.
(좀 더 구체적으로 말하면, 모수에 대한 가정을 하지 않기 때문에 만족시켜야 할 조건이 없다고 보면 되겠습니다)
그렇다면 "비모수 검정으로 모든 테스트를 하는 것이 낫지 않을까요?" 라는 질문이 있을 수 있습니다.
하지만, 비모수 검정의 경우 강력한 통계 검정력(혹은 상관관계에 대한 구체적 정보)을 얻기 어렵다는 단점이 있습니다.
(특히, 모수검정의 조건을 만족할 경우 모수/비모수 검정 양쪽 모두 유의하게 결과가 나오기 쉽기 때문에 이왕이면 정보량이 많은 모수 검정을 사용하는 것이 바람직하겠습니다)
두가지 검정 방식 : "스피어만의 ρ (Spearman's rho)"와 "켄달의 τ (Kendall's τ)"
흥미롭게도, 앞서 말한 데이터에 대한 관점의 차이로 서열형 변수의 상관관계는 두 가지 방식 스피어만의 rho와 켄달의 tau를 같이 사용하는 경우가 많습니다(하나만 제시할 수 있지만, 대부분 같이 적용합니다).
이에 따라 오늘은 두 검정 방식을 모두 사용해 보겠습니다.
스피어만의 rho
이제 비모수 검정의 상관관계 검정 방법 중, 스피어만의 rho를 확인해 보겠습니다.
import pingouin as pg
pg.corr(times.Income, times.Hobby, method="spearman")
혹은, 정리해서 다음과 같이 확인합니다.
import pingouin as pg
pg.corr(times.Income, times.Hobby, method="spearman").round(3)
켄달의 tau
스피어만의 rho와 방법은 비슷합니다.
pg.corr(times.Income, times.Hobby, method="kendall")
같은 방식으로 반올림 처리도 가능합니다.
pg.corr(times.Income, times.Hobby, method="kendall").round(3)
두 검정 모두 p-value가 0.05보다 작기 때문에 검정 값이 유의하다고 할 수 있겠습니다.
특히, 결과를 비교해 보면 실제로 피어슨의 r 보다 정보량이 부족한 것을 확인할 수 있습니다.
2022.08.11 - [데이터과학 기초/통계] - 파이썬으로 상관관계(Correlation analysis) 분석하기 : 피어슨의 r
통계 결과 해석 및 보고
마지막으로 통계 검정 결과를 보고하도록 하겠습니다.
이전 포스팅에서 언급한 바와 같이 다음과 같이 세 요소를 넣어서 문장을 구성하시면 되지만, 이번에는 "비모수 검정"을 사용했기 때문에 추가적인 서술이 필요합니다.
1. 어떤 통계 기법을 사용했는가?
데이터는 서열형 변수를 사용했으며, 이에 따라 상관관계 검증을 위해 비모수 검정을 사용했다.
2. 통계 분석 결과
r = 0.711, p-value<0.005, 신뢰구간 95%에서 [0.64, 0.77]로 두 변수 사이의 관계가 유의하다. (스피어만)
r = 0.579, p-value<0.005, 신뢰구간 95%에서 [0.48, 0.66]로 두 변수 사이의 관계가 유의하다. (켄달)
3. 결과 해석
검정의 결과 ~에 따라(보통 테이블로 두 검정 수치를 같이 정리합니다) 두 변수 사이의 관계가 유의하며, ~의 방향(양수/음수에 따라 결정)을 갖는다.
이렇게 마무리 해 주시면 통계 분석이 마무리됩니다.
'데이터과학 기초 > 통계' 카테고리의 다른 글
| 파이썬으로 분산분석(ANOVA)하기 (2) - Two-Way (이원 분산분석) (0) | 2022.08.25 |
|---|---|
| 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석) (0) | 2022.08.14 |
| 파이썬으로 상관관계(Correlation analysis) 분석하기 : 피어슨의 r (0) | 2022.08.11 |
| 파이썬으로 Chi-Square(카이 제곱)검정 돌리기 (0) | 2022.08.06 |
| 파이썬으로 대응표본 t-test 돌리기 (0) | 2022.08.04 |



