일원 분산분석에서 이원 분산분석으로
지난 시간에는 ANOVA의 기본형인 일원 분산분석(One-Way ANOVA)을 수행하고 보고해 봤습니다.
2022.08.14 - [데이터과학 기초/통계] - 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석)
일원 분산분석은 수많은 논문에 사용되고 여러 방향으로 응용되어 왔는데요.
일원 분산분석이 강력하고 설명하기 편한 방법론 중 하나기 때문입니다.
하지만, 통계 패키지가 편리해지고 데이터 분석이 보편화되면서, 복잡한 모델을 사용하는 케이스가 증가하고 있습니다.
(개인적으로는 데이터 기반 분석에서 머신러닝과 결합한 경과 통계가 과거보다 많이 복잡해졌다고 느낍니다)
이런 배경에서, 통계 분석은 어느 정도 기본기(?)로 갖춰 두는 것이 좋다고 생각합니다.
오늘은 일원 분산분석(One-Way) ANOVA에서 더 나아간 이원 분산분석(Two-Way ANOVA)에 대해 알아보겠습니다.
이원 분산분석의 차이점? - 상호작용
이원 분산 분석의 기본적인 접근은 간단합니다.
일원분산분석이 "하나의 효과(Main Effect, 주 효과)"에 의해 결괏값이 영향을 받았는지 살펴본다면, 이원 분산분석은 "두 개의 효과"가 작용했는지 살펴보는 검정입니다.
얼핏 듣기에는 딱히 차이가 있지 않다고 생각하기 쉽지만, 여기에는 함정이 있습니다.
효과가 하나 더 늘어남으로써 우리는 상호작용효과(Interaction Effect)를 고려해야 하기 때문입니다.
간단히 생각해 볼까요?
우리가 커피 프랜차이즈를 운영하는 과정에서 일일 평균 손님 수 조사를 한다고 합시다.
일반적으로 "지역"이 주요한 매출 차이의 원인이 되지만, 그 외로도 "건물유형"와 같은 요인이 존재할 수 있습니다.
다시 한번 기억을 되살려 볼 때, 우리는 "예측이 빗나가는 정도(분산)"에 미치는 영향이라는 측면에서 효과를 판단했는데요.
2022.08.14 - [데이터과학 기초/통계] - 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석)
두 개 이상의 효과를 측정할 때, 단순한 합 : "A지역이 더 손님 수가 많다" + "~유형의 건물에서 손님 수가 많다"으로만 평가하는 것이 정확한 방법이 될까요?
아니면 "A지역에서는 ~건물 유형에서 장사하는 것이 손님 수가 많다!"과 같은 상호작용을 고려하는 것이 더 정확할까요?
아주 특별한 경우가 아니라면 "상호작용"을 보는 것이 중요하다는 것을 눈치챌 수 있을 겁니다.
실제로 우리 주변에는 "하나의 효과"가 아닌 "두 개 이상의 상호작용"이 영향을 주는 사건들이 많이 관찰됩니다.
(e.g. 학습방법 X 연령대, 정치성향 X 소득수준 등 조합은 아주 다양합니다)
그렇다면, 최대한 많은 요인을 한꺼번에 넣고 평가하는 것이 가장 정확하지 않을까요?
라는 질문을 제시한다면, 나중에 배울 공분산분석(ANCOVA)와 다중 회귀분석(Multiple Regression)의 기초적인 접근법을 이해했다고 할 수 있습니다.
이원 분산 분석 vs 반복 측정 분산분석
일반적으로 "일원 분산분석(변수가 한 개) -> 이원 분산분석(변수가 두 개?)"라고 생각하기 쉽습니다.
그러나, ANOVA를 적용하는 과정에서 요인을 어떻게 바라볼 것인지에 따라 분산분석의 종류가 더 세분화될 수 있습니다.
다만, 이원 분산분석에서 가장 중요한 지점은 여러 번 반복(Repeated) 측정된 값(요인)이 ANOVA 모형에 포함되는지 여부입니다.
반복 측정된 값을 사용한 ANOVA의 경우 반복측정 분산분석(RM-ANOVA, Repeated Measures ANOVA)라고 따로 분류하는 경우가 많습니다.
그렇기에, 일반적으로 설명하는 이원 분산분석은 "우리가 중요하게 생각하는 두 요인 + 상호작용"이 미치는 영향을 판단하는 분석법이라고 볼 수 있겠습니다.
(더 복잡한 모델로는 mixed ANOVA와 같은 모델이 있지만, 설명이 길어지므로 오늘은 가장 보편적인 이원 분산분석의 형태를 다루겠습니다)
이원 분산분석의 가설 설정
일원 분산분석의 경우, 가설 설정이 간단했습니다.
"~라는 요인이 종속변인(혹은 결과)에 유의한 영향을 주는가?"
하지만, 2개의 요인을 고려하면서 우리는 좀 더 복잡한 가정을 세울 필요가 생겼습니다.
A와 B라는 요인에 대해 각각의 조합을 고려해야 하기 때문입니다.
A, B, A&B에 따라 우리는 세 개의 가설을 확인할 필요가 있습니다.
- A라는 요인이 유의한가? (대립 가설 : A라는 요인에 따라 결괏값 평균이 달라질 것이다 / 귀무가설 : A라는 요인에 따른 결괏값 평균은 차이가 없을 것이다)
- B라는 요인이 유의한가? (대립 가설 : B라는 요인에 따라 결괏값 평균이 달라질 것이다 / 귀무가설 : B라는 요인에 따른 결괏값 평균은 차이가 없을 것이다)
- A와 B과 상호작용한 것이 유의한가? (대립가설 : A 요인 별 결괏값 평균은 B에 따라 달라질 것이다 / 귀무가설 : A 요인 별 결괏값 평균은 B에 따라 달라지지 않을 것이다)
일원(One-Way) 분산분석에 비해 생각할게 정말 많아졌습니다.
하지만, 걱정할 필요는 없습니다. 이원 분산분석에서 여러분들이 눈여겨 보아야 할 것은 A와 B의 상호작용입니다.
(반대로 말하면, A와 B가 각각 유의해도 A&B가 유의하지 않다면 골치가 아파진다는 이야기입니다....)
이원 분산 분석의 접근법
이원 분산분석의 경우 일반적으로 두 개의 모델을 검증하는 방식으로 통계 분석을 수행합니다.
- A와 B가 유의하지만, A&B가 유의하지는 않다고 가정한 모델
- A와 B, 그리고 A&B가 유의한 모델
일단 1 vs 2를 통해서 어떤 쪽이 정확한 지 확인하고, 그다음으로 1 중에서 A나 B 어느 쪽이 유의한 지 혹은 둘 다 유의한지 살펴보는 것입니다.
(더 섬세하게 모델/대비 계획을 구성한다면 매우..... 어렵게 처리할 수 있지만 기본적인 구성은 모델 간의 비교로 생각하는 편이 편합니다)
다만, 오늘은 기본적인 형태의 Two Way ANOVA를 수행하는 만큼 2번 모형을 기본으로 검증을 진행해 보도록 하겠습니다.
(실제로, 몇몇 서적들이 1 -> 2 비교 대신 2번을 바로 수행하는 경우가 많습니다. 하지만, 정석적인 접근은 모델에 변수를 넣어가면서 최적의 모델을 추론하는 방식을 취해야 한다는 사실을 기억해 주세요)
패키지 설치
제 포스팅을 꾸준히 보셨다면 알 수 있지만, 통계에는 항상 세 가지(데이터 분석, 시각화, 통계) 역할을 하는 패키지가 필요합니다.
오늘은 좀 복잡한 작업을 하기 때문에, 여러 가지 패키지를 한 번에 사용해야 합니다.
다음과 같이 설치를 진행해 주세요. 혹시 conda 설치를 모른다면 pip로 설치하거나, 아래 포스팅을 참조해 주시길 바랍니다.
2022.07.31 - [데이터과학 기초/Python배우기] - conda로 손쉽게 파이썬 환경 관리하자 (Intel부터 M1까지) - 기초
Two-Way ANOVA의 경우 사후검정(Post Hoc) 등에서 추가 작업이 필요하기 때문에 설치를 두 단계로 진행하겠습니다.
일단 데이터 확인 및 통계 검정을 위한 패키지를 설치합니다.
# conda 사용할 경우
conda install -c conda-forge seaborn pandas statsmodels pingouin
# pip 사용할 경우
pip install seaborn pandas statsmodels pingouin
그다음으로 사후검정 등의 작업을 위한 추가 패키지를 설치하겠습니다
conda로 설치할 경우 에러가 나는 경우가 있으니, conda를 쓰더라도 pip로 설치해 주시길 바랍니다.
(물론 사후검정 등을 하지 않을 경우 굳이 설치할 필요는 없습니다)
pip install bioinfokit
* 현재 파이썬 conda 환경이 주 사용 환경이라 오류가 나면 안될 경우, 임시로 환경을 하나 더 만들어서 설치 테스트 해 보시길 바랍니다
샘플 데이터 로드
일단, 아래 샘플 데이터를 다운받아 파이썬 폴더에 넣어주세요.
샘플 데이터는 1) 지역 2) 마케팅 전략(1+1 vs 2+1)에 따른 판매량 변화 데이터 입니다.
데이터가 로드됐다면, 간단히 로드 결과를 확인해 보도록 합시다.
import pandas as pd
Selling = pd.read_csv("Selling.csv")
Selling
별문제 없이 로드됐고, 전체 120 지점에, 3개의 컬럼이 확인됩니다.
기술 분석과 시각화
항상 강조하지만, 통계 분석을 시행하기 전에 데이터의 특징을 확인하기 위해 기술 분석을 수행할 필요가 있습니다.
다음과 같이 간단하게 describe() 명령을 구성하여 각 그룹별 기술분석을 수행해 보겠습니다.
만약, Groupby 명령어가 이해가 되지 않는다면, 이전 포스팅을 참조해 주세요.
2022.08.06 - [데이터과학 기초/통계] - 파이썬으로 Chi-Square(카이 제곱)검정 돌리기
변수 별 그룹을 생성한 후, describe()를 수행할 경우 결괏값은 다음과 같이 확인됩니다.

이제, 평균값과 분산을 알았으니 이상치나 직관적인 차이를 확인하기 위해 시각화가 필요합니다.
지금까지는 밀도함수 등을 사용했지만, 그룹이 많아질 경우 가독성을 해치기 쉽기에 박스플롯을 그려보겠습니다.
박스플롯은 시각화할 그룹이 많을 경우 매우 효율적으로 데이터의 전체 특징을 파악하게 해 줍니다.
박스플롯 에 들어갈 변수 중, y축을 종속변수로 놓고 나머지 값을 그룹 구분에 사용하여 코드를 구성해 보겠습니다.
sns.boxplot(x="Place", y="Sales", hue="Marketing", data=Selling)
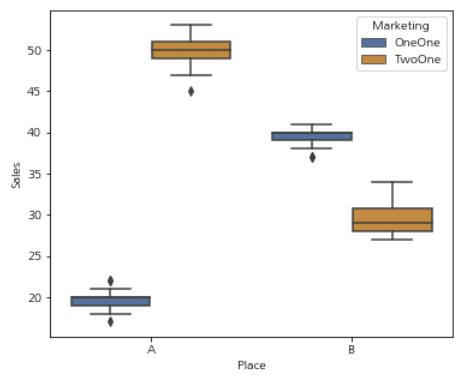
시각화 결과, 큰 폭의 차이(아웃라이어, 결측치)가 확인되지 않기 때문에 바로 통계 분석을 시행해 보겠습니다
* ANOVA를 위한 가정(등분산, 정규성 등)은 이전 시간에 이미 다뤘기 때문에 시간 관계상 이전 포스팅을 참조해 주시면 되겠습니다.
2022.08.14 - [데이터과학 기초/통계] - 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석)
통계 검정
ANOVA 자체가 복잡한 통계 검정 방법이 아니기 때문에, 명령은 간단합니다.
이전 시간에 설명한 바와 같이 statsmodels이 분석 과정에서 장점을 가지기 때문에, statsmodels를 기본으로 검정을 진행해 보도록 하겠습니다.
Statsmodels의 사용법이 기억나지 않는다면, 이전 포스팅을 참조해 주세요.
2022.08.14 - [데이터과학 기초/통계] - 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석)
이전과 같은 조건에서 우리는 1) 장소 영향 2) 마케팅 영향 3) 장소와 마케팅 영향 세 조건을 모두 확인해야 합니다.
이 경우, 간단하게 별(*) 표시로 3가지 경우를 모두 포괄하여 표현할 수 있습니다(경우에 따라 콜론 : 으로 표기하기도 합니다).
말로 하면 애매하지만, 실제로 보면 간단합니다.
# 패키지 로드
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# 모델 설정
model = 'Sales ~ Marketing*Place'
# 모델 피팅
two_anova = ols(model, data=Selling).fit()
# 결과 테이블 확인
anova_lm(two_anova)
ANOVA 테이블의 해석은 이미 이전 포스팅에서 다뤘기 때문에, 같은 맥락에서 확인하면 됩니다.
F값과, p 값을 확인한 후, 유의한 p값(0.05 아래)을 가진 요인을 유의하다고 판단하면 됩니다.
굳이 편의를 고려하자면, 소수점 조절 정도는 할 수 있겠습니다.

다만, 여기서 눈여겨보아야 할 것은 "두 요인의 상호작용항(Marketing:Place)"이 유의하다는 것입니다.
두 상호작용항이 유의할 경우, 다른 두 요인의 영향보다는 상호작용에 해석의 중심이 맞춰져야 하기 때문입니다.
왜 그럴까요? 이는 시각화를 통해 이해할 수 있습니다.
ANOVA 결과 시각화
결과 시각화는 간단하게 seaborn을 통해 각 카테고리 별 평균의 차이를 선으로 이어 보면 분명하게 나타납니다.
두 요인의 영향이 각각 유의하다면 평행한 두 선이 그려져야 하지만, 결괏값은 "교차하는 선"이 만들어졌습니다.
import seaborn as sns
sns.pointplot(x="Place", y="Sales", hue = 'Marketing',data=Selling)
이것은 "장소에 따라 다른 마케팅 전략이 손님을 증가시킨다는 점"을 보여줍니다.
즉, 두 요인보다 두 요인의 결합이 더 중요하다는 해석이 이뤄질 수 있습니다.
(반대로 상호작용이 유의하지 않다면, 두 요인 중 손님을 가장 잘 유인할 수 있는 각각의 요인만 확인하면 됩니다)
사후 검정 (Post Hoc) 테스트
위에서 제기한 "각각 어떤 차이가 존재하는가?"에 대한 질문을 보여주기 위해 마지막으로 사후 검정을 실행합니다.
Two-Way ANOVA의 경우 사후검정 과정에서 사용하는 함수인 PairwiseTukeyHSD가 두 요인을 입력값으로 받기 어렵기 때문에 이를 지원하는 패키지인 bioinfokit를 사용해서 검정을 수행하면 됩니다.
from bioinfokit.analys import stat
result = stat()
result.tukey_hsd(df=Selling, res_var='Sales', xfac_var=['Place',"Marketing"], anova_model=model)
result.tukey_summary
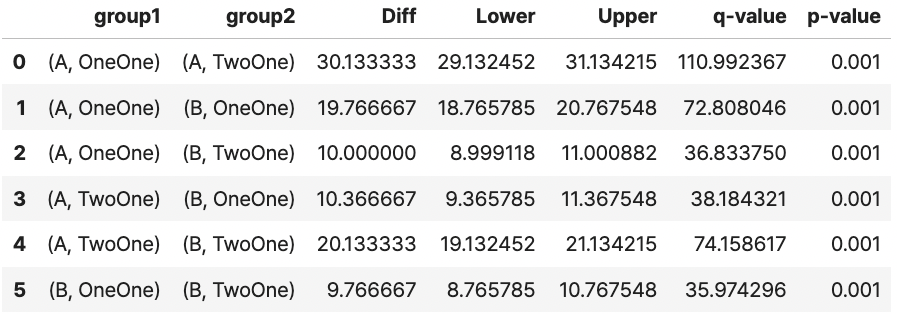
같은 방식으로 [장소, 마케팅] 요인을 각각 사후 검정 할 수 있습니다.
다만, 그룹이 2개기 때문에 Tukey는 실질적인 의미가 없다고 볼 수 있다고 생각하여 코드만 적어놓도록 하겠습니다.
# 장소 기반 검정
result = stat()
result.tukey_hsd(df=Selling, res_var='Sales', xfac_var='Place', anova_model=model)
result.tukey_summary
# 마케팅 기반 검정
result = stat()
result.tukey_hsd(df=Selling, res_var='Sales', xfac_var='Marketing', anova_model=model)
result.tukey_summary
결과 보고
지금까지 통계의 결과 보고는 주로 글과 통계치에 맞춰져 있었습니다.
하지만, 위에서 보듯이 ANOVA의 결과와 해석은 데이터 양이 많기 때문에 글로 표현하는데 한계가 있습니다.
그렇기 때문에 이번 분석을 1) 이원 분산분석(Two-Way ANOVA)의 사용 여부 2) 검정 결과 3) 사후 검정
을 중심으로 "표"와 그림의 내용을 내용을 적절히 해석해서 아래와 같이 보고서에 넣어주면 되겠습니다.
이원 분산분석을 한 결과 (특정 변수 집합)가 유의하게 나타났다. (유의한 변수 1)는 통계량 (테이블 값)로 유의했고, (유의한 변수 2)는 통계량 (테이블 값)로 유의했다. 다만 (유의하지 않은 변수)는 유의하게 나타나지 않았다.
세부적인 내용으로는 사후검정 (사후검정 방식, Tukey 등) 에 따라 (사후검정 조합)가 (테이블 값)으로 유의하게 높았다/낮았다.
일반적으로 1) 기술 분석 결과(표) 2) ANOVA 검정 결과(표) 3) 박스 플롯 시각화 4) 사후 검정 (+시각화?)가 요구됩니다.
다만, 각 분야마다 미묘하게 요구 정보가 다르기 때문에 관련 분야의 보고서나 논문을 반드시 확인해 보시길 바랍니다.
(예를 들어 ANOVA 결과 테이블에서 모든 값의 합을 추가 행으로 적어놓는 경우라든지 조금씩 차이가 존재합니다)
추가 정보/학습
이번 포스팅의 길이와 내용에서 알 수 있듯 일원 분산분석을 포함하여 심화된 분산분석은 통계학에 대한 배경 없이 간단히 코딩으로 이해하기엔 큰 장벽이 존재합니다. 코드대로 따라 한다면 결과 확인은 가능하지만, 검정 과정에 대한 설명과 해석이 보고에 큰 비중을 차지하기 때문입니다 (이는 나중에 다룰 회귀분석과 연결되는 지점입니다).
예를 들어, 1) 샘플 수가 다를 경우, 2) 요인의 조합이 더 복잡할 경우 3) 2에 더해 상호작용이 없거나 일부만 존재할 경우 4) 등분산 등의 조건을 만족하지 못할 경우 등등 수많은 조건/목적의 차이가 있다면 어떻게 검정 방법을 변화시켜야 할까요?
이런 디테일과 해석은 결과적으로 통계 기법에 대한 전반적인 지식을 요구합니다.
그렇기에 분산분석의 메커니즘을 구체적으로 알고 싶거나, 더 정확한 내용을 설명하거나 제시해야 하는 경우 반드시 전문 지식을 추가로 확인하시길 바랍니다.
'데이터과학 기초 > 통계' 카테고리의 다른 글
| 파이썬으로 공분산분석(ANCOVA) 수행하기 (2) | 2022.09.24 |
|---|---|
| 최소한의 통계로 p-value 이해해 보기 (2) | 2022.09.01 |
| 파이썬으로 분산분석(ANOVA)하기 (1) - One Way (일원 분산분석) (0) | 2022.08.14 |
| 파이썬으로 상관관계(Correlation analysis) 분석하기 : 스피어만의 rho / 켄달의 tau (0) | 2022.08.12 |
| 파이썬으로 상관관계(Correlation analysis) 분석하기 : 피어슨의 r (0) | 2022.08.11 |



